講座主題：Vertex stabilizers of symmetric graphs and their applications
主講人： 郭松濤
工作單位：河南科技大學(xué)
活動時間：2020年12月13日 15:40-16:30
講座地點：騰訊會議,，會議ID：850 153 808
主辦單位：煙臺大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院
內(nèi)容摘要：
A graph, with a group 
of its automorphism, is said to be 
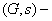transitive, if G is transitive on 
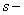arcs but not on 
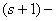arcs of the graph. Let X be a connected 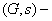transitive graph, and let 
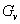be the vertex stabilizer of a vertex 
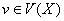in . In 1980, Djokovic and Miller gave the exact structure of 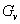for the cubic case, and Weiss and Potocnik gave such structure for the tetravalent case. In this talk, we will discuss the structure of 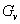for the pentavalent and hexavalent cases, and give the idea of the main proof. Also, with the similar method, we can get such structures for the valency 7 and 8.
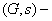transitive graph is also simply called symmetric graph or arc-transitive graph. A graph is called edge-primitive if the full automorphism group of the graph is primitive on edges. The structure of the vertex stabilizer 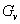plays an important role in the study of 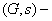transitive graph. As we all known that except for a star graph, all the edge-primitive graphs are arc-transitive. We will introduce the method about how to use the structure of 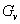to determine the edge-primitive graphs with small valencies, and also some symmetric graphs of certain order and valency.
主講人介紹：
郭松濤，副教授,。2009年廣西大學(xué)碩士畢業(yè),，導(dǎo)師徐尚進教授。2012年北京交通大學(xué)博士畢業(yè),，導(dǎo)師馮衍全教授?，F(xiàn)就職于河南科技大學(xué)-數(shù)學(xué)與統(tǒng)計學(xué)院，從事代數(shù)圖論,、置換群論和組合網(wǎng)絡(luò)等方面的研究,。主持國家自然科學(xué)青年基金1項，河南科技大學(xué)青年學(xué)術(shù)技術(shù)帶頭人培育項目1項,。在J.Combin.Theory B, J. Algebraic Combin., Electronic J. Combin., Discrete Math., Algebra Colloquium, Acta Math. Appl. Sinica English Series等國內(nèi)外著名期刊上發(fā)表論文30余篇.
